Authors

The sort was presented in 2002 by three mathematicians from the University of Auckland, New Zealand. They are Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen. They work in such fields as discrete mathematics, the theory of number, quantum computations, the information theory and combinatorial algorithms.
 I’m not sure, which one of them was the first to come up with the idea. Perhaps, Calude, since he also professes the History of Computing Mathematics. Everybody knows that the progenitor of counting in Europe was abacus. It moved on from Babylon to Egypt, then to Greece, Rome and, finally, the whole Europe. The appearance and operating principle of the ancient “calculator” is reminding of the “simple” sort behavior so much that it’s sometimes called Abacus sort.
I’m not sure, which one of them was the first to come up with the idea. Perhaps, Calude, since he also professes the History of Computing Mathematics. Everybody knows that the progenitor of counting in Europe was abacus. It moved on from Babylon to Egypt, then to Greece, Rome and, finally, the whole Europe. The appearance and operating principle of the ancient “calculator” is reminding of the “simple” sort behavior so much that it’s sometimes called Abacus sort.Algorithm

Suppose, we need to sort out a set of natural numbers. We’ll place each number one under another in the form of a horizontal row from the appropriate number of beads. Now let’s take a look at these bead groups not horizontally, but vertically. Move the beads down to the stop. Now count the beads in each horizontal row. We’ve got a primary set of numbers and it’s ordered.
Implementation
You will find the Bead sort in more than 30 programming languages here. Despite the fact that the algorithm looks pretty simple, the implementation is not that trite.Degenerated Case

It’s a reversely ordered array. A maximum number of beads will have to fall down from the highest points.
Limited Applicability
This method can be applied mostly to natural numbers.We can also sort integers, but it’s more complicated, since we’ll have to process negative numbers separately from positive ones.
Nothing prevents us from sorting fractional numbers. But we should cast them to integers before that (for instance, multiply everything by 10^k, sort it out, and then divide by 10^k)
Also, we can definitely sort strings, if we represent each of them as a positive number. But what for?
Time Complexity
There are four sorting complexities, depending on the context we consider the algorithm in.O(1)

It’s an abstract case, a spherical Bead sort in the vacuum. Imagine that all beads moved simultaneously and take their places. This complexity cannot be implemented in practice or the algorithm theory.
O(√n)
It’s the estimation for the physical model, in which beads slide down along the greased spokes. The time of free fall is proportional to the square root of the maximum height, which is proportional to n.O(n)
The beads that haven’t reached their places are moved one row at a time. This complexity is appropriate for physical devices that implement such sorting and also analogous or digital hardware implementations.O(S)

S – is the sum of the array elements. Each bead is moved on individually. They are not moved in groups simultaneously. It’s an adequate evaluation of the complexity for implementation in programming languages.
Memory Complexity
It leaves much to be desired. Bead sort is the record-holder as for waste. The costs for the extra memory exceed the costs for storing the array itself. They’re O(n2) on overage.Physics
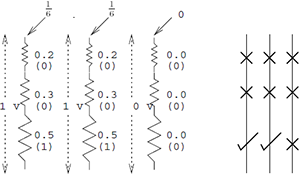
The presence or absence of beads can be interpreted as the analogue voltage going through a series of electric resistors. Poles that are used to move the beads are analogues of electric resistors, in which voltage increases downwards.
If you’re an expert in electrostatics, please refer to this document(PDF).
In Practice
Bead sort – is a form of a sort by counting. The number of beads in each vertical row is the number of elements in an array. The elements are equal to or bigger than the order number of the vertical.Characteristics of the Algorithm
Name: Bead sort; Abacus sortAuthors: Joshua J. Arulanandham, Cristian S. Calude and Michael J. Dinneen
Year of publication: 2002
Class: Distribution Sort
Stability: Stable
Comparisons: No comparisons
Time Complexity: O(1), O(√n), O(n), O(S)
Memory Complexity: O(n^2)
References
- Bead Sort at the website of the University of Auckland
- The authors’ documentation of the algorithm(PDF)
- Implementation in various programming languages
- Bead sort in the Wikipedia
The authors’ homepages:
0 comments
Upload image