Reading an article about getting a job in ABBYY, I came across the following task:
Find the Nth Fibonacci Number in O(N) time of arithmetic operations.
Thinking about it, I realized that the only solutions coming to my mind were those operating in O(n) time. But I found a better solution later.
I am going to use the following denotation of sets:
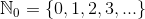 - non-negative integers
- non-negative integers
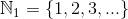 — positive integers
— positive integers
According to various mathematic traditions, a set of natural numbers can either contain 0 or not. Therefore, it’s preferred to indicate it explicitly in international mathematic texts.
The Solution
Donald E. Knuth provides a matrix identity of the following form:
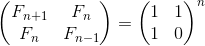
The identity is provided without any proof, but it’s quite easy to prove it by induction.
The matrix on the right is called Q-matrix.
Let’s indicate:
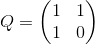
According to the identity, 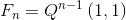 . Thus, to calculate
. Thus, to calculate 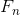 , we should calculate
, we should calculate 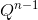 matrix and take the first element of the first line (the enumeration starts with 1).
matrix and take the first element of the first line (the enumeration starts with 1).
Since 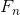 calculation comes to raising the matrix to power, let’s take a look at this process in details.
calculation comes to raising the matrix to power, let’s take a look at this process in details.
Let's say there is a 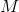 matrix to be raised to
matrix to be raised to 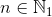 power. Suppose,
power. Suppose, 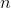 is the power of 2. Thus,
is the power of 2. Thus, 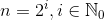 .
.
We can represent 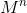 in the form of a tree:
in the form of a tree:
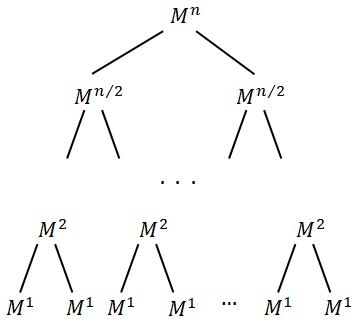
Meaning that:
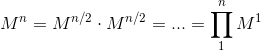
So, to calculate 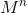 matrix, we should calculate
matrix, we should calculate 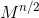 matrix and multiply it by itself. To calculate
matrix and multiply it by itself. To calculate 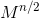 we would have to do the same with
we would have to do the same with 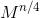 and so on.
and so on.
Obviously, the tree height is 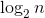 .
.
Let’s estimate 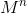 calculation time.
calculation time. 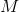 matrix is of the same size in any power. Therefore, we can perform the multiplication of two matrices in any power in
matrix is of the same size in any power. Therefore, we can perform the multiplication of two matrices in any power in 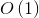 . We should perform
. We should perform 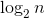 of such multiplications. So,
of such multiplications. So, 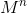 complexity is
complexity is 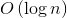 .
.
But what if n is not a power of 2?
There is a question now: what should we do if 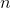 is not a power of 2? We can factor down any natural number
is not a power of 2? We can factor down any natural number 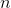 as a sum of numbers that are the power of 2, without any repetitions (we do it all the time when converting a number from a binary to decimal numeral system). I.e.:
as a sum of numbers that are the power of 2, without any repetitions (we do it all the time when converting a number from a binary to decimal numeral system). I.e.:
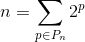
where 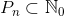 is a set of powers, with the help of which we express
is a set of powers, with the help of which we express 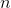 . Remembering that
. Remembering that 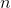 is the power of a matrix, we get:
is the power of a matrix, we get:
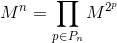 .
.
Matrix multiplication is not commutative though, i.e. the order of operands during the multiplication is important. But the commutative property is kept for the so-called permutation matrices. Matrix 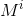 is permutational for
is permutational for 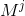 ,
, 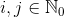 . Thus, we will not have to consider the order of operands during the multiplication task, which simplifies the process a bit.
. Thus, we will not have to consider the order of operands during the multiplication task, which simplifies the process a bit.
So, we can represent the algorithm of 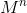 calculation if the form of the following two steps:
calculation if the form of the following two steps:
- Factor down
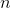 into the sum of the powers of two in the form of
into the sum of the powers of two in the form of 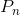 .
. - Calculate all the elements of
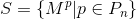 set.
set. - Calculate
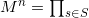 .
.
Let’s estimate the execution time of the given algorithm.
The first step performs in 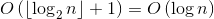 , where
, where 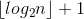 is the number of binary digits in
is the number of binary digits in 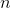 .
.
Since we have to perform no more than 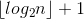 matrix exponentiation, the second step takes
matrix exponentiation, the second step takes 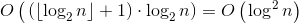 time.
time.
The third step performs in 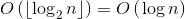 , as we should multiply matrices no more than
, as we should multiply matrices no more than 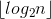 times.
times.
Optimization
Is it possible to improve the algorithm execution time? Yes, it is. You should note that the second step does not describe the method of calculating matrices that belong to 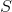 set. We know that
set. We know that 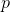 is the power of 2 for each of them. Getting back to the picture with the tree, it means that all of them lie in some or other tree tiers and to calculate the greater ones, we should calculate the inferior ones. If we apply Memoization technique and cache all the calculated matrices of every tier, this will allow us to shorten the execution time of the second step up to
is the power of 2 for each of them. Getting back to the picture with the tree, it means that all of them lie in some or other tree tiers and to calculate the greater ones, we should calculate the inferior ones. If we apply Memoization technique and cache all the calculated matrices of every tier, this will allow us to shorten the execution time of the second step up to 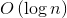 , as well as the total execution time of a whole algorithm. That’s exactly what we need according to the task.
, as well as the total execution time of a whole algorithm. That’s exactly what we need according to the task.
The Code
Let’s get down to coding. I implemented the algorithm in Python due to the following reasons:
- It’s expressive enough to replace the pseudo code
- Its arbitrary-precision arithmetic is clear.
It’s going to look like this:
class MatrixFibonacci:
Q = [[1, 1],
[1, 0]]
def __init__(self):
self.__memo = {}
def __multiply_matrices(self, M1, M2):
"""Matrices miltiplication
(the matrices are expected in the form of a list of 2x2 size)."""
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
r = [[a11, a12], [a21, a22]]
return r
def __get_matrix_power(self, M, p):
"""Matrix exponentiation (it is expected that p that is equal to the power of 2)."""
if p == 1:
return M
if p in self.__memo:
return self.__memo[p]
K = self.__get_matrix_power(M, int(p/2))
R = self.__multiply_matrices(K, K)
self.__memo[p] = R
return R
def get_number(self, n):
"""Getting the nth Fibonacci number
(a non-negative integer number is expected as n)."""
if n == 0:
return 0
if n == 1:
return 1
# Factoring down the passed power into the powers that are equal to the power of 2),
# i.e. 62 = 2^5 + 2^4 + 2^3 + 2^2 + 2^0 = 32 + 16 + 8 + 4 + 1.
powers = [int(pow(2, b))
for (b, d) in enumerate(reversed(bin(n-1)[2:])) if d == '1']
# The same, but less pythonic: http://pastebin.com/h8cKDkHX
matrices = [self.__get_matrix_power(MatrixFibonacci.Q, p)
for p in powers]
while len(matrices) > 1:
M1 = matrices.pop()
M2 = matrices.pop()
R = self.__multiply_matrices(M1, M2)
matrices.append®
return matrices[0][0][0]
mfib = MatrixFibonacci()
for n in range(0, 128):
num = mfib.get_number(n)
print(num)Benchmarks
I wanted to compare the execution time of my algorithm with a classical iteration algorithm that is based on the consecutive 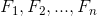 calculation saving the previous two numbers. I implemented it like this:
calculation saving the previous two numbers. I implemented it like this:
def get_number(self, n):
if n == 0:
return 0
a = 0
b = 1
c = 1
for i in range(n-1):
c = a + b
a = b
b = c
return c
I used the following technique of performance testing.  number accepts
number accepts 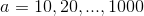 values. Objects of MatrixFibonacci and IterationFibonacci (it’s the class that calculates Fibonacci numbers iteratively) classes are created for each
values. Objects of MatrixFibonacci and IterationFibonacci (it’s the class that calculates Fibonacci numbers iteratively) classes are created for each  . Then, an arbitrary
. Then, an arbitrary 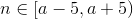 integer is generated 10 000 times.
integer is generated 10 000 times.
The test outputs a lot of strings like: n
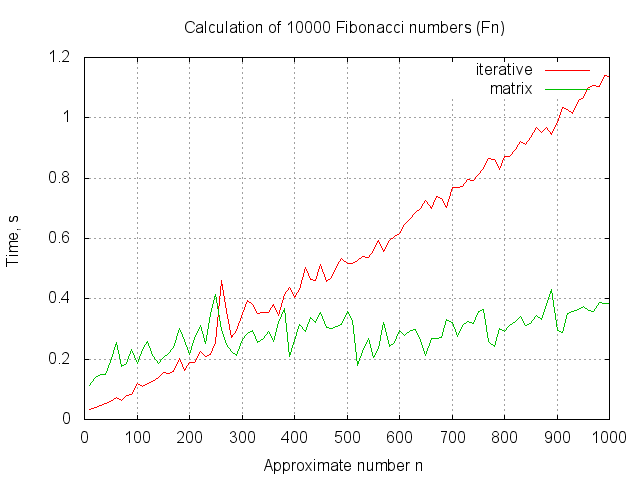
As you can see from the chart, the matrix algorithm leaves the iterative algorithm behind starting from 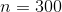 (its worth noting that
(its worth noting that 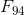 will not fit into unsigned 64 bits). I guess, it's possible to say that the algorithm is impractical, though its theoretical speed is quite good.
will not fit into unsigned 64 bits). I guess, it's possible to say that the algorithm is impractical, though its theoretical speed is quite good.
You will find the complete source code with the benchmark here.
The code for gnuplot to build charts:
set terminal png
set output 'fibgr.png'
set grid
set style data linespoints
set title "Calculation of 10000 Fibonacci numbers (Fn)"
set xlabel "Approximate number n"
set ylabel "Time, s"
plot "benchmark.txt" using 1:2 with lines title 'iterative', \
"benchmark.txt" using 1:3 with lines title 'matrix'References
- Donald E. Knuth. The Art of Computer Programming. Volume 1. Fundamental Algorithms.
11 comments
The power function is also not O(1) in n. You would get the same runtime O(log(n)) with a clever implementation.
You can be a little more concise with the code by modifying how __memo is set up.
Then you can do:
I know it essentially does the same thing, IMHO it's a little cleaner code thou ;)
Around 1000 gives Iterative: 0.054137468338 Matrix: 1.92105817795
This all stays in memory for my machine.
You can find the improved fork of your code here:
gist.github.com/ClashTheBunny/762a497d920a24aada69
*cap obvious flies away*
I made a benchmark that shows that in practice:
docs.google.com/spreadsheets/d/1mDIuAUrI6lzZxDf2HEqHbaYjddfK0hijd_r9qBOOEoQ
Suppose that we know that t^2 = t + 1 for some t. (Equivalently, we'll work in the quotient ring R = Z[t]/(t^2 — t — 1).) Now, let's look at the powers of t. By using the rule that t^2 = t + 1, we will end up with only units and coefficients of t. (That this is the characteristic polynomial of the matrix discussed in the main article is, of course, not a coincidence.)
t^0 = 1
t^1 = t
t^2 = t + 1
t^3 = t^2 + t = (t + 1) + t = 2 t + 1
t^4 = 2 t^2 + t = 2 (t + 1) + t = 3 t + 2
t^5 = 3 t^2 + 2 t = 3 (t + 1) + 2 t = 5 t + 3
Hmm. There's a pattern: t (a t + b) = a t^2 + b t = a (t + 1) + b t = (a + b) t + a. I feel a theorem coming on: t^k = F_k t + F_{k-1} for all integers k. Proof. (a) t^1 = t = F_1 t + F_0. (b) Suppose the claim holds for k; then t^{k+1} = t t^k = (F_k + F_{k-1}) t + F_k = F_{k+1} t + F_k. (c) Notice that t (t — 1) = t^2 — t = (t + 1) — t = 1, so t^{-1} = t — 1; then, supposing again that the claim holds for k, we have t^{k-1} = (t — 1) (F_k t + F_{k-1}) = F^k t^2 + F_{k-1} t — F_k t — F_{k-1} = F_k (t + 1) + F_{k-1} t — F_k t — F_{k-1} = F_{k-1} t + (F_k — F_{k-1}) = F_{k-1} t + F_{k-2}, as required. []
Now, we can compute powers of t using the ordinary square-and-multiply method (or fancier methods involving windowing, combs, or whatever). The important pieces are:
(a t + b)^2 = a^2 (t + 1) + 2 a b t + b^2 = (2 a b + a^2) t + (a^2 + b^2) t
(a t + b) (c t + d) = a c (t + 1) + (a d + b c) t + b d = (a d + a c + b c) t + (a c + b d)
Here's a simple left-to-right exponentiation algorithm. Suppose we want to compute x^n, and we know that n = 2^k u + v, for 0 <= v < 2^k, and x^u = y. (Initially, we can arrange this with 2^k > n, so u = 0, v = n, and x = 1.) Now, suppose that v = 2^{k-1} b + v', where b is either zero or one, and v' < 2^{k-1}. Let u' = 2 u + b. Then n = 2^{k-1} u' + v', and x^{u'} = x^{2u+b} = y^2 x^b. Continue until k = 0.
Annoyingly, this means we need to count the number of bits in n, i.e., k = L(n), with 2^{i-1} <= n < 2^i. We can start with an upper bound, finding the smallest 2^{2^j} > n. Suppose, inductively, that we know how to determine L(m) for 0 <= m < 2^i, and that n < 2^{2i}. If n < 2^i, then we're done; otherwise write n = 2^i n' + r where 0 <= r < 2^i. Since n < 2^{2i}, we know that n' <= n/2^i < 2^i, so we can determine k' = L(n'). Let k = k' + i: I claim that 2^{k-1} <= n = 2^i n' + r < 2^k. Taking the lower bound first, we're given that 2^{k'-1} <= n', so 2^{k-1} = 2^i 2^{k'-1} <= 2^i n' <= 2^i n' + r. But also, n' < 2^{k'}, so n' + 1 <= 2^{k'} and 2^i n' + 2^i <= 2^i 2^{k'} = 2^k. But r < 2^i, so n = 2^i n' + r < 2^k as required. []
Enough theory! Now let's turn this into actual code!
Upload image