Being a fan of scientism, I am going to tell you about the nature of time, causality and time travels.
Time
According to classical mechanics, time is absolute and invariable in the sense that when moving from one reference system to another one, time frames do not change:
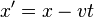



(x, y, z, t) are coordinates in the old frame, while (x', y', z', t') are coordinates in the new one. It is expected that one system moves in-parallel along x axis at v speed.
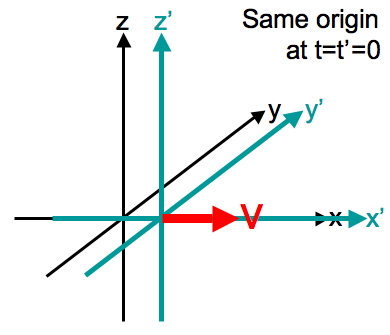
It’s the so-called Galilean transformation, which is what happens to coordinates when reference systems are changed. In the Galilean sense, there’s just one “time flow” in the Universe and time coordinates are the same for all objects. At that, classical mechanics does not treat the time arrow originality in any way. Moreover, the concept of the flow of time does not work with the Newtonian formulas.
By the way, we are the ones to introduce the movement from past to future in classical mechanics. Let’s assume that there is a given set of material points (coordinates and speed) and operating forces. Then we provide dt interval and watch the system evolve in time. We can also move in the opposite direction and see what happened to the system in the past.
But “time travels”, meaning moving from one particular object to the past along t axis, is forbidden by Newtonian mechanics (see above – there’s just one time flow in the Universe).

The situation had changed, when Maxwell introduced electrodynamics and then Einstein created the Special relativity (SR), when trying to solve the contradictions between electrodynamics and classical mechanics.
Within the limits of SR when moving from one inertial reference system to another one, we are going to use the following transformations:
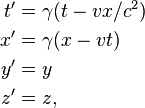
where
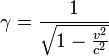
As you can see, each reference system has “its own” time scale. Within the limits of SR, neither space, nor time intervals between points are saved. Only the difference of their squares is.
ds2 = c2dt2 — dx2 — dy2 — dz2
What is written here? It’s a description of the special four-dimensional pseudo-Euclidian space. It’s the so-called Minkowski space, in which the distance between the points is equal to the difference of squares of the coordinate differences (not the sum, as in the regular Euclidian space).
From the point of view of SR, each body movement represents a trajectory in the four-dimensional Minkowski space, the so-called “world line”.
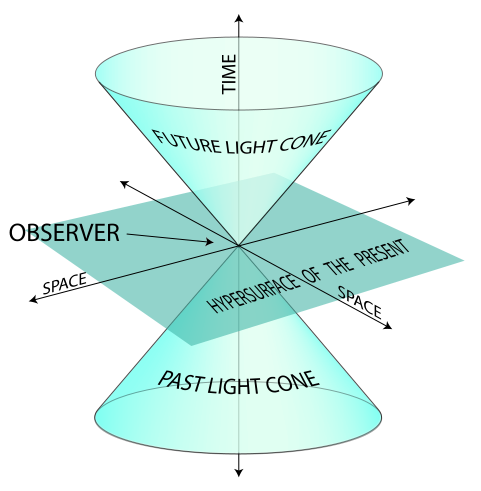
Cones at the picture are the so-called “light cones”. They are trajectories of objects moving at the speed of light.
Since each object has its own time that can change arbitrary, we can theoretically assume that there can be “unfolding” of the world line, meaning time traveling.
In the special theory of relativity (SR), it’s quite simple to travel forward in time. It’s enough to move at the speed that is close to the speed of light. This effect has been confirmed successfully. Therefore, we are going to talk about traveling back in time.
Two Problems
The first one lies in the fact that a material object can never reach the boundary of the light cone, as it would be necessary to apply an infinite amount of energy for that purpose.
The second one lies in peculiarities of Lorentz transformations. Suppose, we have managed to move an object from A point to B faster than the speed of light. Then there will surely be a reference system, in which the object will show up in B point at first and then will leave from A point. Put simply, movement faster than the speed of light is actually traveling in time in SR, but in an extremely nontrivial sense.
But how should we understand the phrase “there will be a system…”? It appears that for a part of observers there are travels back in time, but there aren’t any for another part. It depends on the speed of the observer movements.
Secondly, there’s a complete mess with cause and effect. It is obvious that the object appearing in B point is the effect of it leaving A point. But for some observers the effect takes place later than the cause. But for others it happens earlier. We are going to get back to this question a bit later.
As a result, moving at the speed of light is forbidden in Special Relativity. Or rather, it’s forbidden to transfer information between the objects that are outside the light cone of each other. Otherwise SR faces unsolvable contradictions.
Moving faster than the speed of light is initially permitted, as long as the systems moving faster than light do not exchange any information. For example, according to the theory of Eternal inflation, at the very beginning of the Big Bang the family of newly-born Universes moves away from each other at the speed that exceeds the speed of light. There’s no contradiction here, as all Universes move away from each other faster than light. The light of any of them will never reach another one and the information will never be transferred.
But let’s get back to our talk about the nature of time. To tell the truth, SR did not bring much understanding to this problem. What is “internal time” of an object and how do we measure it? Why is the temporal constant of Minkowski space opposed to spatial ones? Finally, what does the “inertial reference system” mean and where can we get it in reality?
Einstein was the one to understand all of the mentioned difficulties. Therefore, he had invented General relativity that confused everyone even more.
To begin with, all coordinates in General relativity (including temporal one) are just numbers of points on the axis. Since they have no other meaning, you can set any numbers.
It is necessary to determine the so-called fundamental metric tensor — gab in the coordinates for each point of the space-time. What is it? It’s a 4х4 matrix that defines the distance between neighboring points. Suppose you are in some (x0, x1, x2, x3) point and move towards (dx0, dx1, dx2, dx3). You are going to cover the distance like this:
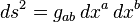
Hereinafter, repeated indices mean summation, i.e. the sum of 16 components is written here.
For the regular Euclidean space with the orthonormal basis the matrix is equal to one. In Minkowski space g00 = 1, g11 = g22 = g33 = -1.
In the General relativity space there can be any components of the metric tensor. The distance between neighboring points is (almost) an arbitrary function of the difference of coordinates. Keep in mind that coordinates are absolutely relative.
If we want to move from one reference system to another one, all tensors, including the fundamental metric one, will undergo the following changes:
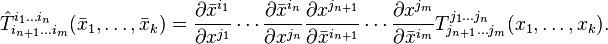
Guess what, this part turns out to be the simplest one :). To cut a long story short, you can assign any coordinates, as well as any reference point in General relativity. The only thing you will have to calculate is the fundamental metric tensor. You can number the moments of time as you like.
We seem to have clarified some things about the space-time geometry. Now, let’s move on to the objects in this space. We should form the so-called Stress-energy tensor (Energy-momentum tensor, Tab) from the distribution of impulses and energies of the bodies. There’s a separate tensor for each point of the space-time. It defines “density” of masses and energies.
Finally, we are going to need derivatives of the fundamental tensor for all directions, as well as derivatives (speeds) of all the objects.
Now, we can state the way geometry of space and moves of bodies influence each other.
The geometry of space is measured the following way:
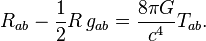
This equation is known as Einstein’s equation. Rab is the so-called Ricci curvature tensor that is expressed via the second partial derivatives of the fundamental metric tensor. (By the way, Grigori Perelman has proved Puankare theorem in his works dedicated to Ricci flow).
What does all of this mean? Knowing the energy-momentum tensor, the metric tensor and its derivatives, we can calculate the second derivatives of the metric tensor. Thus, we are defining the way energy and impulses influence the space geometry.
In order to define the way geometry of space influences the objects moving in it, we direct ds2 → min covered distance for each material point. Expanding this condition with the help of, say, Lagrange–d'Alembert principle, we will get expressions for the second object derivatives (“acceleration”). In particular, for non-mass particles (of light) the motion occurs along the geodesic line that is expressed by the following equation:
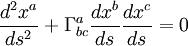
Гabc are Christoffel symbols that are expressed via the metric tensor.
There is quite a smart analogy describing the meaning of such a motion in clear terms. Let’s imagine that we have stretched a sheet and put heavy balls in some parts of it. The sheet has weighed down in these places, just like space distorts when there’s some impulse or energy.

Now, let’s roll a light ball on the sheet. It will move in a straight line on the level parts. But when coming close to massive points, it will crook its trajectory, as if heavy balls have “drawn” it. That is the gravity effect caused by the crook of “space” the ball is moving in.
Okay, let’s sum up the way objects move with regard to General relativity:
- we should know the current geometry of space (the metric tensor) and locations of energies and impulses in it (the energy-momentum tensor);
- we should also know the “speeds”, meaning the first partial derivatives of both of them;
- then we will be able to calculate the second derivatives of the metric tensor, as well as the world lines of objects, and make a modeling step.
To tell the truth, it is not that simple to set some initial state of the system. It can turn out that this location is unacceptable. There’s no algorithm allowing to construct the state. The sum of two acceptable states can turn out to be the unacceptable state. There are four accurate analytic solutions of Einstein’s equations: Schwarzschild, Kerr, Reissner–Nordström and Kerr–Newman metrics describing space with one material spinning/non-spinning charged/non-charged point.
Numerical solution of equations is not either possible due to their complexity. We would have to store four 16-digit matrices for each point of the four-dimensional space and solve 32 equations during each step. Considering modern capacities, it would be impossible.
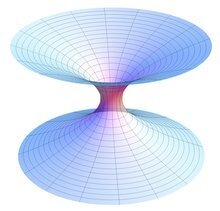
Anyway, let’s get down to more particular questions. Does General relativity forbid the motion with time decrease? It does not. Directing ds2 → min, we can get dt < 0 in some conditions for the optimal motion trajectory. To tell the truth, it’s not simple to formalize “some conditions”. For instance, we can suppose that there exist such a phenomenon as “wormholes”. They are peculiar distortions of the space geometry that allow to travel (perhaps, safely even for humans) at speeds faster than the light speed (which is, in some way, traveling back in time).
Has General relativity clarified the nature of time? On the one hand, space, time, energy and impulse have acquired new meanings within the limits of the theory. On the other hand, questions to General relativity are not clearly formed, just like in Newtonian mechanics. For instance, all the General relativity is covariant. It is written with the help of tensors with subscripts (tensors with superscripts are called contravariant). By the way, I forgot to mention that we cannot change the location of an index for no reason as it will change the expression for transfer from one coordinate system to another one. But the reason General relativity is contravariant is one of philosophical questions that are not simple to realize, let alone answering them.
Taking a look at such modern theories as String ones, we can say that they are more or less about the same. But they operate not on the four-dimensional, but on the 10- or even 11- dimensional space, in which all dimensions, except four, “folded” so that their size is null for us. Multidimensional surfaces are considered in this space (branes are multidimensional membranes). String-objects move on the surfaces. An object moves in a way, so that its trajectory would not “sweep” the minimal “area” on the “brane” surface. The sense is approximately the same, but there are more dimensions.

We could also talk about Quantum mechanics, but, to tell the truth, it’s beyond me. There’s almost nothing interesting about it there. Quantum mechanics is more classical than General relativity in this regard. Its laws are obviously written like derivatives with time. Besides, the temporal coordinate of an object, just like the spatial one, subordinates to the indeterminacy principle and we cannot determine it accurately together with energy.
Now, let’s get back to the causality principle. We can see that General relativity does not provide any insight here. As if there’s no causality. But we do know that it exists and can see it in the world provided in sensations.

General Theory of Relativity (and String theories) have complicated everything even more. While Newtonian mechanics did not allow any time travels, General relativity states that the causality principle is the only thing preventing from traveling in time. Nothing forbids time travels mathematically.
To get some scientific reply to this question, we would have to understand the meaning of the causality principle.
There’s a theory deriving from causality as from the basis of the Universe. It’s the so-called theory of Causal dynamical triangulation. You can google it. Alas, there isn’t anything special in the theory, string theories seem more interesting. But some physicists think otherwise. For example, Lee Smolin in his “The trouble with physics: the rise of string theory, the fall of a science, and what comes next”.
So, that’s it. After all, I have disappointed you. I would be really surprised to find out that anything became clearer for you. For instance, the way time is built and whether time travels are possible. To tell the truth, I became more confused when writing this article. But I do hope that now you realize that it’s impossible to solve this question easily by dreaming up some nonsense :).
0 comments
Upload image