A Few Words About Reversible Computing
HaskellToday I would like to raise a topic that has recently become all the more relevant and interesting. At least, judging by all the increasing number of publications in this direction, the interest in it is really growing. I am talking about quantum computing, or, to be more accurate, about a model of quantum computations. Without going into details of the model, let’s take a look at one of numerous questions related to it. We are going to review reversible computing.
Further discussion will be held with the use of examples written in Haskell. To my mind, functional programming is much closer to the model of quantum computations than any other type. Let me leave out the reasoning of my point of view. But to understand the model of quantum computations, we need a much more severe paradigm shift, than, say, a shift from structured programming to object-oriented and even more so to the functional. I am not talking about some programmers being better or worse than others. The new model comprehension is a real revolution in our brain and the way of algorithmic thinking.
So, if you are interested in the topic and you want a little dive into the magical world of quantum computing, you should go on reading. At the end of the article you’ll find a small bonus.
Some Necessary Historic Information
If we pay our attention at the elements of a Boolean algebra, we will see that all the elements of two inputs and one output lose information during the operating process. For instance, AND Boolean function. Its truth table looks like this:
| X | Y | X & Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Rolf Landauer first thought about this aspect of computations in 1961. He was the one to give birth to the principle that connects informational entropy with thermodynamic one. Indeed, a loss of information is associated with the release of heat by physical computing devices.
But what if we implement these computational elements that do not lose information during operation? From the point of view of pure (theoretical) logic, there’s nothing complicated about it. The problem is that we need the elements, with the help of which we could implement any other Boolean function. Like for the basis of standard NOT and OR elements, or the one-element NAND basis.
There have been found invertible elements with this property. In this article we will look at a couple of these elements — Toffoli and Fredkin gates.
Toffoli Gate
The logic Toffoli gate is a Boolean function which has 3-bit inputs and outputs (i.e. f: {0, 1}3 → {0, 1}3). Its truth table is as follows:
| Input | Output | ||||
|---|---|---|---|---|---|
| C1 | C2 | I | C1 | C2 | O = I ⊕ C1C2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |

This function is also known as CCNOT (Controlled-Controlled-NOT). This name takes account of the fact that the logic function NOT is applied to the third I bit if and only if the first two bits are of 1 value. This great function is not only invertible (if we take a closer look at it, there’s a one-to-one mapping between the input and the output threes of values), but it alone can be used to express any other Boolean function. The proof of the fact is really simple. If we fix the value of the input I bit as 1, the function will represent the NAND element that is a basis one.
Let’s try to see it in action. We’ll implement the definition of Toffoli gate in Haskell language. Together with three supplementary service functions, the definition of toffoli function will look as follows:
getX :: (Int, Int, Int) -> Int
getX (x, _, _) = x
getY :: (Int, Int, Int) -> Int
getY (_, y, _) = y
getZ :: (Int, Int, Int) -> Int
getZ (_, _, z) = z
toffoli :: Int -> Int -> Int -> (Int, Int, Int)
toffoli 1 1 0 = (1, 1, 1)
toffoli 1 1 1 = (1, 1, 0)
toffoli x y z = (x, y, z)
There are a very strong simplifications:
- First of all, to represent values of bits, we used Int type, which is not really reasonable. It would be better to use Bool, or even define our own enumeration type for this purpose. But this would be too lengthy to demonstrate. We’ll just take a look at the implementation and that’s it.
- The previous simplification leads to the fact that developers should independently monitor the correctness of values. We can pass 2 and other values to these functions, but these values should not be equal to 0 or 1. Such functions will work successfully in terms of compilation. But we are not going to pass such values, as they are beyond the limits of our consideration. We are only interested in 0 and 1.
- toffoli function returns a tuple of three values. We could also define a special type for this purpose, but let’s leave it this way for simplicity. This fact initiated the definition of getX, getY and getZ service functions.
Now, let’s express all the basic logical operations via Toffoli gate: complementary (NOT), conjunction (AND), disjunction (OR), NAND, NOR, XOR and fan-out operation. It’s worth noting that the last operation is always present in the logic, but we introduce it implicitly.
The functions’ definitions look like this:
not :: Int -> Int
not = getZ . toffoli 1 1
and :: Int -> Int -> Int
and a b = getZ $ toffoli a b 0
nand :: Int -> Int -> Int
nand a b = getZ $ toffoli a b 1
or :: Int -> Int -> Int
or a b = not $ and (not a) (not b)
nor :: Int -> Int -> Int
nor a b = not $ or a b
xor :: Int -> Int -> Int
xor a b = getZ $ toffoli 1 a b
fanout :: Int -> (Int, Int)
fanout a = (getY t, getZ t)
where
t = toffoli 1 a 0
The necessity of using the fan-out operation is absolutely reasonable, as this operation is invertible in the standard logic. As for quantum computations, we cannot branch qubit «wires» just like this, as it’s forbidden by the No-cloning theorem.
The fact that some functions are not expressed via toffoli function does not mean that we cannot express them. We cannot do it with the help of one Toffoli gate, but we can do it via several of them.
Fredkin Gate
Let’s get down to another unit of invertible logic. As well as Toffoli gate, it is invertible and basis.
Thus, we can express any other logic function with the help of it. We’re talking about Fredkin gate. It also has 3-bit inputs and outputs. Its truth table is the following:
| Input | Output | ||||
|---|---|---|---|---|---|
| C | I1 | I2 | C | O1 | O2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
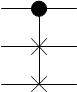
This gate is also known as CSWAP (the Controlled-SWAP). This function exchanges the values of the input I1 and I2 bits only if the value of the controlling C bit is equal to 1. With the help of this gate, we can trivially code such Boolean logic operations as NOT and AND. Therefore, it is basic. That’s how we can code the same functions with the help of it (we have expressed them before via toffoli function):
not' :: Int -> Int
not' a = getZ $ fredkin a 0 1
and' :: Int -> Int -> Int
and' a b = getZ $ fredkin a b 0
nand' :: Int -> Int -> Int
nand' a b = not' $ and' a b
or' :: Int -> Int -> Int
or' a b = not' $ and' (not' a) (not' b)
nor' :: Int -> Int -> Int
nor' a b = not' $ or' a b
xor' :: Int -> Int -> Int
xor' a b = or' (and' b $ not' a) (and' a $ not' b)
fanout' :: Int -> (Int, Int)
fanout' a = (getX f, getZ f)
where
f = fredkin a 1 0
There are the same considerations for this code as for the previous one. Expressing functions via the already defined ones does not affect the fact that all of them are expressed via Fredkin gate.
We should also say that toffoli and fredkin functions are invertible. As for other functions expressed with the help of them, they are not invertible. Why? Because getX, getY and getZ functions lose information; and they are meant this way.
Expressing Toffoli Gate via Fredkin Gate and Vice Versa
Let’s get down to some higher-order cases and express Toffoli gate via Fredkin gate and vice versa. It’s a nice exercise.
It’s no brainer to express Toffoli gate. The first two inputs do not change. As for the third one, there is a primitive propositional formula: O = I ⊕ C1C2. The definition will look like this:
toffoli' :: Int -> Int -> Int -> (Int, Int, Int)
toffoli' x y z = (x, y, xor' z $ and' x y)
I even made a scheme that shows all the beauty of it:

We can see that to express one Toffoli gate, that has three inputs and three outputs via the Fredkin gate, there should be 5 gates to express FANOUT operations (red F rectangles), 5 for AND operation (blue F rectangles) and 4 for NOT operation (green F rectangles). 14 gates altogether with 26 inputs and outputs, and only 3 of them are significant. Thus, 26 bits are “gibberish”. We need them just to provide the reversibility of computations.
This means that when designing circuits of reversible computations, we face the size increase (exponential?) of computational circuits. As a result, to execute such computations, we also need to increase memory. That’s how we pay for reversibility. The question to dispute is whether the necessity of exponential memory increase will become a barrier for quantum computations.
We should also note that the provided above chart is the most direct expression being really non-optimized. It goes without saying that with the use of special circuit design techniques this chart can be minimized in terms of the number of gates used. But this number will still be quite big.
As for expressing Fredkin gate via Toffoli gate, it’s going to be more complicated. It has two output bits that have more complicated propositional formula. But it’s not that difficult anyway:
fredkin' :: Int -> Int -> Int -> (Int, Int, Int)
fredkin' x y z = (x, xor y s, xor z s)
where
s = and x $ xor y z
An interested reader can try to make a chart and count the number of Toffoli gates and gibberish bits in it.
That’s pretty much it.
A Small Bonus
Let’s think about Schrödinger’s cat. Why could not Erwin Schrödinger explain the “paradox”? He was the one who wrote “What is Life? The Physical Aspect of the Living Cell.”

It’s all about perception. Only a living being can perceive (even an ameba). Perception is an act of measurement that destroys the superposition. Putting a cat in a box, Schrödinger also placed “the means of measurement” in a box. A photon, being in the superposition of quantum states after overcoming the semitransparent mirror, enters the box and the detector in this state. At that very moment, the cat’s system of perception destroys the superposition. And it’s not about consciousness. It’s all about perception.
When there is a photon in a superposition and it falls into a kind of measuring device (not a living, just a measuring one), the device itself enters the superposition in “the photon is located” – “the photon is not located”. But I can be wrong. Roger Penrose was the one to be planning to check this paradox. I’m not sure, whether he has succeeded in it, but he will not put cats in boxes for sure.
Or what is it? The Observer’s problem?
Ropes — Fast Strings

Comments
Chris Silvia
Roman V. Dushkin
Chris Silvia
Roman V. Dushkin