Lock-free Data Structures. The Inside. Memory Management Schemes
C++As I’ve already mentioned in the previous articles, the main difficulties when implementing lock-free data structures are ABA problem and memory reclamation. I will separate these two problems even though they are connected as there are algorithms that can solve only one of them. In this article I am going to review popular methods of safe memory reclamation for lock-free containers. I’ll demonstrate the application of one or another method of the classic lock-free queue by Michael-Scott [MS98].
Tagged pointers
Tagged pointers is a scheme introduced by IBM for to solve the ABA problem. Perhaps, it’s the most popular algorithm for this problem’s solution. According to this scheme each pointer represents an atomic pair of the memory cell address and its tag (32-bit integer number).
template
struct tagged_ptr {
T * ptr ;
unsigned int tag ;
tagged_ptr(): ptr(nullptr), tag(0) {}
tagged_ptr( T * p ): ptr(p), tag(0) {}
tagged_ptr( T * p, unsigned int n ): ptr(p), tag(n) {}
T * operator->() const { return ptr; }
};
A tag is a version number and is incremented at every CAS operation on a tagged pointer and is never reduced, strictly growing. When you delete an element from a container instead of physically removing the element you should place it into some list of free elements (a free-list). It’s quite possible that there will be a call to the deleted element, which is in the free-list. Our structures are lock-free so while one thread deletes X element, another thread can have a local copy of the tagged pointer and refer to the element fields. So there should be a separate free-list for each T type. In many cases it’s quite illegal to call the destructor of T type data when placing the element into the free-list (due to parallel access. During destructor operations another thread can read the data of this element). The tagged pointer scheme has the following drawbacks:
- The scheme is implemented at platforms, which have an atomic CAS primitive over a double word (dwCAS). This requirement is fulfilled for 32-bit modern systems as dwaCAS operates with 64-bit words while all modern architectures have a complete set of 64-bit instructions. But 128-bit (or at least 96-bit) dwCAS is required for 64-bit operation mode. It isn’t implemented in all architectures. > Stuff and nonsense! > Experienced lock-free programmers can object that it isn’t necessary to have a wide 128-bit (or 96-bit) CAS for tagged pointers implementation. You can do with 64-bit considering the fact that modern processors use 48 bit only for addressing, older 16 bit addresses are free and you can use them for the tag counter, like in boost.lockfree. > But there are two snags to this approach: > > - Who guarantees that these 16-bit addresses won’t be used in future? As soon as there’s another breakthrough in the area of memory chips and its volume rises steeply the vendors will at once introduce new processors with the complete 64-rank addressing. > - Are 16 bit enough for the tag storage? Some researches have been carried out in this respect. They showed the following result: 16 bit are not enough, overflow is quite possible and it can potentially lead to ABA problem. While 32 bit are enough. > > > And really, 16 bit is a value of the tag 0 – 65535. In modern operational systems the time slice for a thread is about 300 – 500 thousands of assembler instructions (taken from internal correspondence of Linux developers). When processor performance grows the time slice can only grow as well. So it’s quite possible to execute 65 thousands of even such difficult operation like CAS (if it’s not possible today, it will be tomorrow). Thus, by using 16-bit tag we’re risking of facing an ABA problem.
- Free-list implementation is a lock-free stack or lock-free queue. This fact brings in a negative contribution to performance: at least one more CAS call when removing the element from the free-list and adding to it. On the other hand, with free-list availability can contribute to performance increase. Whereas the free-list isn’t empty it isn’t necessary to refer to system functions which are usually slow and synchronized of memory allocation.
- Availability of a separate free-list for every data type can be an unattainable luxury for some applications as it can lead to inefficient memory use. For example, if a lock-free queue consists of 10 elements on the average but its size can increase up to 1 million, the free-list size after the spike can be about 1 million. Such behavior is often illegal.
So tagged pointer scheme is an example of the algorithm that can solve ABA problem only. It can’t solve the problem of memory reclamation. For the moment libcds doesn’t use tagged pointers for the implementation of lock-free containers. Despite the relative simplicity this scheme can lead to unmanageable growth of used memory due to lock-free availability for every container-object. In libcds I focused on lock-free algorithms with predictable memory use, without applying dwCAS. boost.lockfree library is a good example of applying the tagged pointers scheme.
An Example of Tagged Pointers Use
For those who prefer wallpapers (if there are any) there’s MSQueue [MS98] pseudocode with the tagged pointer. Yes, lock-free algorithms are verbose indeed! I left out std:atomic application for simplicity.
template struct node {
tagged_ptr next;
T data;
} ;
template class MSQueue {
tagged_ptr volatile m_Head;
tagged_ptr volatile m_Tail;
FreeList m_FreeList;
public:
MSQueue()
{
// Allocate dummy node
// Head & Tail point to dummy node
m_Head.ptr = m_Tail.ptr = new node();
}
void enqueue( T const& value )
{
E1: node * pNode = m_FreeList.newNode();
E2: pNode–>data = value;
E3: pNode–>next.ptr = nullptr;
E4: for (;;) {
E5: tagged_ptr tail = m_Tail;
E6: tagged_ptr next = tail.ptr–>next;
E7: if tail == Q–>Tail {
// Does Tail point to the last element?
E8: if next.ptr == nullptr {
// Trying to add the element in the end of the list
E9: if CAS(&tail.ptr–>next, next, tagged_ptr(node, next.tag+1)) {
// Success, leave the loop
E10: break;
}
E11: } else {
// Tail doesn’t point to the last element
// Trying to relocate tail to the last element
E12: CAS(&m_Tail, tail, tagged_ptr(next.ptr, tail.tag+1));
}
}
} // end loop
// Trying to relocate tail to the inserted element
E13: CAS(&m_Tail, tail, tagged_ptr(pNode, tail.tag+1));
}
bool dequeue( T& dest ) {
D1: for (;;) {
D2: tagged_ptr head = m_Head;
D3: tagged_ptr tail = m_Tail;
D4: tagged_ptr next = head–>next;
// Head, tail and next consistent?
D5: if ( head == m_Head ) {
// Is queue empty or isn’t tail the last?
D6: if ( head.ptr == tail.ptr ) {
// Is the queue empty?
D7: if (next.ptr == nullptr ) {
// The queue is empty
D8: return false;
}
// Tail isn’t at the last element
// Trying to move tail forward
D9: CAS(&m_Tail, tail, tagged_ptr(next.ptr, tail.tag+1>));
D10: } else { // Tail is in position
// Read the value before CAS, as otherwise
// another dequeue can deallocate next
D11: dest = next.ptr–>data;
// Trying to move head forward
D12: if (CAS(&m_Head, head, tagged_ptr(next.ptr, head.tag+1))
D13: break // Success, leave the loop
}
}
} // end of loop
// Deallocate the old dummy node
D14: m_FreeList.add(head.ptr);
D15: return true; // the result is in dest
}
Let’s look attentively at the algorithms before enqueue and deueue operations. By their example you can see several standard approaches of lock-free structures building.
It draws attention that both methods contain loops — all the content part of operations is repeated until it’s successfully executed (or successful execution is impossible; for example, dequeue from a empty queue). Such repeating with the help of the loop is a typical method of lock-free programming.
The first element in the queue (to which m_Head points) is a dummy node. Dummy node presence guarantees that the pointers to the queue beginning and end will never be NULL. The sign of an empty queue is _Head == m_Tail && m_Tail->next == NULL condition (D6-D8 lines). The last (m_Tail->next == NULL) condition is significant as when adding to the queue we don’t change m_Tail, E9 line just changes m_Tail->next. So at first glance, enqueue method breaks the queue structure. In fact, the change of m_Tail tail takes place in a different method and/or a different thread. enqueue operation checks up (E8 line) before adding the element that m_Tail points to the last element (m_Tail->next == NULL). If this is the case it tries to move the pointer to the end of the line (E12 line). dequeue before executing its responsibilities also changes m_Tail, if it points to the end of the line (D9 line). This demonstrates a popular approach in lock-free programming: threads mutual help (helping). An algorithm of one operation is “spread” to all container operations and one operation hopes that the following operation call (maybe, another one) will finish its work in (maybe) another thread.
Another fundamental observation: operations store in local variables the pointers values which they need for their operation (E5-E6, D2-D4 lines). Then (E7, D5 lines) just calculated values are compared with originals. It’s a typical lock-free method and it’s unnecessary for the non-concurrent programming as since the moment of read the original values can change. If you don’t want the compiler to optimize the access to shared data of the queue (too “clever” compiler can even delete E7 or D5 lines of comparison), you should declare m_Head и m_Tail in C++11 as atomic (volatile in pseudocode). We should also remember that CAS primitive compares the destination address value with the given one. If they’re equal it changes the data to the new value according the destination address. So for CAS primitive it’s necessary to indicate the local copy of the current value. CAS(&val, val, newVal) will almost always be successful, which is an error for us.
Now let’s consider the situation when in dequeue method data copying takes place (D11 line): before removing the element from the queue (D12 line). Taking into account that element (moving m_Head forward in D12) deletion can fail the data copying (D11) can be repeated. From a C++ point of view it means that the data stored in the queue shouldn’t be too complex or the burdens on assignment operator will be too great. So CAS primitive failure is more possible in conditions of high load. A try to “optimize” the algorithm by taking D11 line outside the loop limits will lead to an error: next element can be deleted by another thread. Whereas the considered implementation is based on tagged pointer scheme, in which elements are never deleted, such “optimization” will lead to the situation when we can return the wrong data (not those being present in the queue at the moment of D12 line successful execution).
Peculiarities of M&S queue MSQueue is really interesting as m_Head always points to dummy node, and the first element of a non-empty queue is the next after m_Head element. At dequeue the first element, m_Head.next, is read from a non-empty queue. The dummy element is deleted and the following element becomes the next dummy element (and its head). It’s the element, the value of which we return. So we can physically add the element after the next dequeue operation only. This peculiarity can cause much troubles if you want to use the intrusive variant of cds::intrusive::MSQueue queue.
Epoch-based reclamation
Fraser [Fra03] introduced a scheme based on epochs. In this variant we apply delayed deletion at the safe moment when we’re absolutely sure that none of threads has references to the deleted element. Epochs provide such guarantee. There’s a global nGlobalEpoch epoch and each thread works in its local nThreadEpoch epoch. When entering the code guarded by the epoch-based scheme the local epoch of the thread is incremented if it doesn’t exceed the global epoch. As soon as all threads reach the global epoch nGlobalEpoch is incremented. The scheme pseudocode:
// global epoch
static atomic m_nGlobalEpoch := 1 ;
const EPOCH_COUNT = 3 ;
// TLS data
struct ThreadEpoch {
// global epoch of the thread
unsigned int m_nThreadEpoch ;
// the list of retired elements
List m_arrRetired[ EPOCH_COUNT ] ;
ThreadEpoch(): m_nThreadEpoch(1) {}
void enter() {
if ( m_nThreadEpoch The emptied elements of the lock-free container are place into local for the thread list of m_arrRetired[m_nThreadEpoch % EPOCH_COUNT]elements waiting for deletion. As soon as all the threads have passed through the global m_nGlobalEpoch epoch you can empty all lists of all the threads of m_nGlobalEpoch — 1 epoch and increment the global epoch itself. Every operation of the lock-free container is enclosed in ThreadEpoch::enter() and ThreadEpoch::exit() calls; it’s very similar to the critical section:
lock_free_op( … ) {
get_current_thread()->ThreadEpoch.enter() ;
. . .
// lock-free operation of the container.
// we’re inside “the critical section” of the epoch-based scheme,
// so we can be sure that no one will delete the data we’re working with.
. . .
get_current_thread()->ThreadEpoch.exit() ;
}
The scheme is quite simple and protects local references (references inside the container operations) to the elements of lock-free containers. The scheme can’t provide protection of global references (outside container operations). So we can’t implement the concept of iterators by elements of lock-free container with the help of epoch based scheme. The scheme’s drawback is the fact that all threads of the program should move to the following epoch, i.e. they should refer to some lock-free container. If at least one thread doesn’t go to the following epoch there will be no deletion of retired elements. If the threads priority aren’t the same, low-priority threads can bring about an uncontrolled growth of the high-priority threads elements that are delayed for deletion. Thus the epoch based scheme can lead (it will necessary lead in case of one of the threads failure) to the unlimited memory consumption.
libcds library doesn’t have implementations of the epoch based scheme as I didn’t manage to built quite an effective algorithm in order to define whether all threads had reached the global epoch. Maybe, readers could recommend some solution?
Hazard pointer
The scheme is introduced by Michael [Mic02a, Mic03] and is meant for protection of local references to elements of the lock-free data structure. Perhaps, it’s the most popular and studied scheme of delayed deletion. It’s based on atomic read and write only and doesn’t use any “heavy” synchronization primitives of CAS type. The scheme corner stone is duty to declare the pointer to an element of the lock-free container as hazard inside operation of the lock-free data structure. So before working with the element we should place it HP array of current thread hazard pointers. HP array is private for the thread as owner thread only can write in it, but all threads can read it (in Scan procedure). Having attentively analyzed operations of various lock-free containers, I noticed that the size of HP array (the number of one thread hazard pointers) didn’t exceed 3-4. So burdens on scheme support aren’t great.
Huge data structures It’s fair to say that there are “huge” data structures requiring more than 64 hazard pointers. I can cite skip-list (cds::container::SkipListMap) as an example. It’s a stochastic data structures. As a matter of fact, it’s the list of the lists, with a variable level of each element. Such containers don’t fit Hazard Pointer scheme, though there’s a skip-list implementation for this scheme in libcds.
The pseudocode of Hazard Pointers scheme [Mic02]:
// Constants
// P : number of threads
// K : number of hazard pointers in one thread
// N : the total number of hazard pointers = K*P
// R : batch size, R-N=Ω(N), for example, R=2*N
// Per-thread variables:
// the array of Hazard Pointer thread
// Owner-thread only can write in it
// all threads can read it
void * HP[N]
// the current size of dlist (values 0..R)
unsigned dcount = 0;
// an array of data ready for deletion
void* dlist[R];
// Data deletion
// Places data to dlist array
void RetireNode( void * node ) {
dlist[dcount++] = node;
// If the array is filled we call the basic Scan function
if (dcount == R)
Scan();
}
// The basic function
// deletes all elements of dlist array, which haven’t been declared
// as Hazard Pointer
void Scan() {
unsigned i;
unsigned p=0;
unsigned new_dcount = 0; // 0 .. N
void * hptr, plist[N], new_dlist[N];
// Stage 1 – traverse all HP of all threads
// collect the total plist array of protected pointers
for (unsigned t=0; t HP ;
for (i = 0; i When deleting a RetireNode(pNode) element of pNode lock-free container j thread places pNode to the local (for j thread) dlist list of retired(requiring deletion) elements. As soon as the size of dlist list is R (R comparable with N = P*K, but more N; for example, R = 2N), we call Scan() procedure which is in charge of deleting retiredelements. R > P*K condition is essential as only if this condition is fulfilled we can guarantee that Scan() will be able to delete something from the list of retireddata. If this condition is broken Scan() can’t delete anything from the array and we’ll get an algorithm error as the array is completely filled but we can’t reduce it’s size.
Scan() consists of four stages. - At first we prepare plist array with the current hazard pointers. We include in the list all divergent from null hazard pointers of all threads. The first stage only can read the shared data – arrays of HP threads – all other stages work with local data only. - Stage 2 sorts plist array in order to optimize the following search. Here we can also delete tally-elements from plist. - Stage 3 – deletion itself. We scroll all elements of dlist array of the current thread. If dlist[i]element is in plist (some thread is working with this pointer) you can’t delete it and leave it in dlist (relocate to new_dlist). You can delete dlist[i] if no thread is working with it. - Stage 4 copies non-deleted elements from new_dlist to dlist. Whereas R > N, Scan() procedure will necessarily reduce the size of dlist array, i.e. some elements will be deleted without fail.
As a rule, declaring a pointer as HP is carried out the following way:
std::atomic atomicPtr ;
…
T * localPtr ;
do {
localPtr = atomicPtr.load(std::memory_order_relaxed);
HP[i] = localPtr ;
} while ( localPtr != atomicPtr.load(std::memory_order_acquire));
We read atomicPtr atomic pointer to the localPtr local variable (we’ll work with it later) and to the free HP[i] slot of HP array of the current thread hazard pointers. After that we should check up that while we were reading atomicPtr its value hadn’t been changed by another thread. In order to perform the checkup we read atomicPtr one more time and compare it with the read before localPtr value. It happens that way until we place the true (at the moment of declaring it as hazard) value of atomicPtr into HP array. While the pointer is in the array of Hazard Pointers (i.e. it’s declared as hazard) it can’t be deleted physically by any thread. So reference by the pointer won’t lead to reading hash or writing to the free memory area.
Hazard pointers (HP) scheme is analyzed in details with relation to C++ atomic operations and memory ordering in [Tor08] work.
MSQueue performed by Hazard Pointer Lock-free queue by Michael Scott [MS98] performed by Hazard Pointer. I’m providing the “pure” pseudocode here, without libcds specific features.
template
class MSQueue {
struct node {
std::atomic next ;
T data;
node(): next(nullptr) {}
node( T const& v): next(nullptr), data(v) {}
};
std::atomic m_Head;
std::atomic m_Tail;
public:
MSQueue()
{
node * p = new node;
m_Head.store( p, std::memory_order_release );
m_Tail.store( p, std::memory_order_release );
}
void enqueue( T const& data )
{
node * pNew = new node( data );
while (true) {
node * t = m_Tail.load(std::memory_order_relaxed);
// declaring the pointer as hazard. HP – thread-private array
HP[0] = t;
// necessarily verify that m_Tail hasn’t changed!
if (t != m_Tail.load(std::memory_order_acquire) continue;
node * next = t->next.load(std::memory_order_acquire);
if (t != m_Tail) continue;
if (next != nullptr) {
// m_Tail points to the last element
// move m_Tail forward
m_Tail.compare_exchange_weak(
t, next, std::memory_order_release);
continue;
}
node * tmp = nullptr;
if ( t->next.compare_exchange_strong(
tmp, pNew, std::memory_order_release))
break;
}
m_Tail.compare_exchange_strong( t, pNew, std::memory_order_acq_rel );
HP[0] = nullptr; // zero the hazard pointer
}
bool dequeue(T& dest)
{
while true {
node * h = m_Head.load(std::memory_order_relaxed);
// Setup the Hazard Pointer
HP[0] = h;
// Verify that m_Head hasn’t changed
if (h != m_Head.load(std::memory_order_acquire)) continue;
node * t = m_Tail.load(std::memory_order_relaxed);
node * next = h->next.load(std::memory_order_acquire);
// head->next also mark as Hazard Pointer
HP[1] = next;
// If m_Head hasn’t changed – start everything anew
if (h != m_Head.load(std::memory_order_relaxed))
continue;
if (next == nullptr) {
// The queue is empty
HP[0] = nullptr;
return false;
}
if (h == t) {
// Help enqueue method by moving m_Tail forward
m_Tail.compare_exchange_strong( t, next,
std::memory_order_release);
continue;
}
dest = next->data;
if ( m_Head.compare_exchange_strong(h, next,
std::memory_order_release))
break;
}
// Zero the Hazard Pointers
HP[0] = nullptr;
HP[1] = nullptr;
// Place the old queue head into the array of data ready for deletion.
RetireNode(h);
}
};
Is the Hazard Pointer scheme multipurpose? Can it be applied to all data structures? Not in the described above form, as the number of hazard pointers is limited by K constant. For most data structures the condition of limited hazard pointers number is fulfilled, and the number of HP is usually pretty small. But there are algorithms, for which estimating the number of concurrently required hazard pointers is impossible. Sorted Harris list [Har01] can be used as an example. In the algorithm of removing the element from this list a chain of indefinite length can be deleted, which makes HP scheme inapplicable.
Strictly speaking, we can generalize the HP scheme in case of unlimited number of hazard pointers. This scheme author provides detailed instructions how to do it. But I’ve decided to limit myself in libcds to the classic algorithm in order not to complicate the HP scheme and make its implementation more difficult. Especially as there is another less popular scheme – Pass the Buck – which is quite similar to Hazard Pointer. But in this scheme the approach of hazard pointers unlimited number is used. I’ll tell about it later.
Hazard Pointer Implementation in libcds
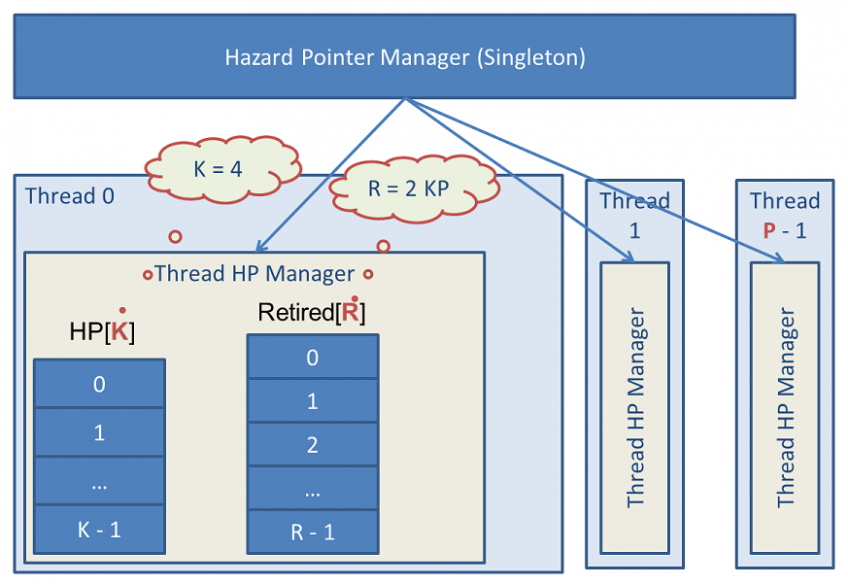This picture demonstrates the inner build of hazard pointer algorithm in libcds. The core of the algorithm – Hazard Pointer Manager – represents a singleton, which is taken out to libcds.dll/.so dynamic library. Every thread has an object – Thread HP Manager framework – where HP array of K size and an array of Retired pointers of R size are located. All strcutures of Thread HP Manager are bound into a list. The maximum number of threads is P. In libcds on default:
- The size of hazard pointers array is K = 8
- Number of threads is P = 100
- The size of retired (ready for deletion) data R = 2 * K * P = 1600.
HP scheme is implemented in libcds in the form of three stages: - Core – is an independent from data type low level implementation of the scheme (namespace cds::gc::hzp). Whereas the core isn’t typified (doesn’t depend on the T type of the data being deleted) it can be taken out to the dynamic library. Information about the data type is lost here, so we can’t call data destructor (it’s fair to mark that “deletion” isn’t always physical. For example, for intrusive containers it’s the call of the disposer functor. It’s a stimulation of “data can be safely deleted” event. We don’t know, what event processor is behind it. - Implementation Level – is a typified implementation of the scheme. It’s located in the namespace cds::gc::hzp. This level represents a set of template of the core shell structures which are called to save data typification (it’s somehow similar to type erasure). This level shouldn’t be used in programs. - The Interface Level (API) – cds::gc::HP class. It should be used (and is used) in lock-free containers of libcds. Actually, it’s the parameter value (one of values, as there are other schemes as well) of GC container template. From the code point of view cds::gc::HP class is a thin wrapper around the implementation level with its scores of small classes.
Reconstructing the lost data type If we’ve “lost” the data type in the core, how is destructor call or rather type reconstruction is executed? It’s simple: every log of the array ready for deletion in the core (time delayed, retired) looks like the following:
struct retired_ptr {
typedef void (* fnDisposer )( void * );
void * ptr ; // Retiredpointer
fnDisposer pDisposer; // Disposer function
retired_ptr( void * p, fnDisposer d): ptr(p), pDisposer(d) {}
};
So retired pointer and the function of its deletion are stored. Scan() method of HP scheme calls pDisposer(ptr) to “delete” the element. pDisposer function knows its argument type. Implementation level is in charge of “transparent” forming of the given function. For example, physical deletion can be carried out the following way:
template
struct make_disposer {
static void dispose( void * p ) { delete reinterpret_cast(p); }
};
template
void retire_ptr( T * p )
{
// Place p into arrRetired array of ready for deletion data
// Note that arrRetired are private data of the thread
arrRetired.push( retired_ptr( p, make_disposer::dispose ));
// we call scan if the array is filled
if ( arrRetired.full() )
scan();
}
This approach is a bit simplified, but I guess the idea is clear.
If you want to use containers on the basis of HP scheme from libcds library, it’s enough to just declare the object of cds::gc::HP type in main() and connect it to every thread using containers that are based on HP scheme. It’s quite another matter if we need to write our own container class based on cds::gc::HP. In this case we should know API of HP scheme.
API of cds::gc::HP class All methods of cds::gc::HP class are static, which accents that the class is a wrapper over singleton. - The Constructor
HP(size_t nHazardPtrCount = 0,
size_t nMaxThreadCount = 0,
size_t nMaxRetiredPtrCount = 0,
cds::gc::hzp::scan_type nScanType = cds::gc::hzp::inplace);
nHazardPtrCount – is the maximum number of hazard pointers (K constant of the scheme) nMaxThreadCount – is the maximum number of threads (P constant of the scheme) nMaxRetiredPtrCount – the array dimension of retired pointers (R constant = of 2KP scheme) nScanType – small optimization: cds::gc::hzp::classic value points out that we should necessarily follow the pseudocode of Scan algorithm. cds::gc::hzp::inplace value allows to get rid of new_dlist array in Scan() and use dlist instead of it (as it can descend only). We should keep in mind that there can be just one cds::gc::HP object. The constructor actually calls static functions in order to initialize the core. So trying to declare two objects of cds::gc::HP class won’t lead to creating two Hazard Pointer schemes, but to recurring initialization, which is safe, but useless. - Placing the pointer to the retired array (time delayed deletion) of the current thread
template
static void retire( T * p ) ;
template
static void retire( T * p, void (* pFunc)(T *) )
Disposer argument (or pFunc) defines the deleting functor (disposer)
In the first case the call is quite pretentious:
struct Foo { … };
struct fooDisposer {
void operator()( Foo * p ) const { delete p; }
};
// Calling myDisposer disposer for the pointer at Foo
Foo * p = new Foo ;
cds::gc::HP::retire( p );
static void force_dispose();
The forced call of Scan() algorithm of Hazard Pointer scheme. I’m not sure what it can be useful for in real life, but it’s sometimes necessary in libcds.
Besides that, three important sub classes are declared in cds::gc::HP class:
- thread_gc – represents a wrapper around the code of initializing the private thread data, referring to Hazard Pointer scheme. This class represents only the constructor, which carries out connection of HP scheme to the thread, and destructor disconnecting the thread from the scheme
- Guard –hazard pointer itself
- template GuardArray – the array of hazard pointers. When applying HP scheme it’s often required to declare several hazard pointers at a time. It’s better to do it in one array at a time, not in several objects of Guard type.
Guard and GuardArrayclasses represent a superstructure over the internal Hazard Pointer array, which is private for the thread. They work as allocators from this internal array.
Guard class is the essence of hazard slot and has the following API:
template
T protect( CDS_ATOMIC::atomic const& toGuard );
template
T protect( CDS_ATOMIC::atomic const& toGuard, Func f );
Declaring an atomic pointer (T type is usually the pointer) as hazard. There’s a loop hidden inside these methods. I’ve described it before. We read the value of toGuard atomic pointer, assign it to the hazard pointer and then check up that the read pointer hasn’t changed. The second syntax (with Func functor) is necessary when we need declare as hazard not the pointer to T *, but some pointer derived from it. It’s a specific character of intrusive containers, in which the container manages the pointers to the node and the pointer to the real data may not differ from it (for example, node can be the field of real data). Func functor has the following signature:
struct functor {
value_type * operator()( T * p ) ;
};
Both methods return the pointer they have declared as hazard.
template
T * assign( T * p );
template
T * assign( cds::details::marked_ptr p );
These methods declare p as hazard. There’s no loop, in contrast to protect. We just relocate p to the hazard slot.
The second syntax is meant for marked cds::details::marked_ptr pointers. The lower 2-3 bits (which are always 0 at the leveled data) are used in marked pointers as a storage of bit flags. It’s a very popular method in the lock-free programming. It places the pointer with cleared flag bits to the hazard slot (by Bitmask mask).
Methods return the pointer which they have declared as hazard.
template
T * get() const;
Read the value of the current hazard slot. It’s sometimes necessary. void copy( Guard const& src );
Copy the hazard slot value from src to this. As a result, two hazard slots contain the same value. void clear();
Zero the hazard slot value. The destructor of Guard class does the same.
GuardArray class has similar API, but an index is also indicated in the array.
template
T protect(size_t nIndex, CDS_ATOMIC::atomic const& toGuard );
template
T protect(size_t nIndex, CDS_ATOMIC::atomic const& toGuard, Func f )
template
T * assign( size_t nIndex, T * p );
template
T * assign( size_t nIndex, cds::details::marked_ptr p );
void copy( size_t nDestIndex, size_t nSrcIndex );
void copy( size_t nIndex, Guard const& src );
template
T * get( size_t nIndex) const;
void clear( size_t nIndex);
An alert reader will notice an unknown word CDS_ATOMIC. What’s that? It’s a macro declaring the appropriate namespace for std::atomic. If compiler supports (and implements) C++11 atomic, CDS_ATOMIC is std. If it doesn’t support, then it’s a cds::cxx11_atomics namespace. In the next version of libcds it’ll be possible to use boost.atomic when CDS_ATOMIC is boost.
Hazard Pointer with Reference Counter
The drawback of Hazard Pointer scheme is that it’s meant for guarding local references only to the nodes of the lock-free container. It can’t guard the global references, necessary for, say, implementing the concept of iterators. An unlimited size of hazard pointers array would be necessary for it.
Specifying As a matter of fact, we can implement iterators using HP scheme. For that the iterator-object should contain a HP slot protecting the iterator pointer. As a result, we’ll get quite a specific iterator bound to the thread (let’s remember that hazard slots a private data for this thread). Considering this fact and also the finite set of hazard pointers, we can conclude that it’s impossible to implement iterators with the help of HP scheme. Classical Greek programmers thought that reference counting is a multi-purpose instrument saving from all errors. But we know now that the ancients were mistaken.
The most popular method to recognize whether the object is being used is reference counting method (RefCount). In the works of Valois – one of pioneers of the lock-free approach – the scheme based on reference counting has been used for the safe deletion of container elements. But RefCount scheme has some drawbacks. The main of them is difficult implementation of circular data structures, when elements refer to each other. Besides, many researchers mark the inefficiency of RefCount scheme as its lock-free implementation uses примитивы fetch-and-add primitives too often (actually, before every use of the pointer the number of counters of references to it should be increased, and they should be decremented after it).
The Study Group of Gothenburg University published its work [GPST05] in 2005. In this work Hazard Pointer and RefCount methods are combined. Hazard Pointers scheme is used for the efficient guarding of the local references inside the operations of lock-free data structures, while RefCount is used for guarding of global references and keeping the data structure integrity.
Let’s name this scheme HRC (Hazard pointer RefCounting). Applying Hazard Pointers has allowed to avoid difficult operations if incrementing/decrementing the number of references to the element. It increases efficiency of RefCounting scheme on the whole. On the other hand, applying two methods at a time somewhat complicated the algorithm of the combined scheme (I’m not providing its complete pseudocode due to abundance of technical details, refer to [GPST05]). While Hazard Pointers scheme doesn’t need any special support from the elements of lock-free container, HRC relies on the presence of two helper methods for the element:
void CleanUpNode( Node * pNode);
void TerminateNode( Node * pNode);
The TerminateNode procedure zeros inside the pNode element all pointers to other container elements. We use CleanUpNode procedure to be sure that pNode element refers to “living” elements only (not marked for deletion) of the data structure, changing (moving forward) the references when necessary. Whereas every reference in RefCount container is accompanied by increase of the element reference counter we refer to, CleanUpNode also reduces reference counters of deleted elements:
void CleanUpNode(Node * pNode)
{
for (all x where pNode->link[x] of node is reference-counted) {
retry:
node1 = DeRefLink(&pNode->link[x]); // set HP
if (node1 != NULL and !is_deleted( node1 )) {
node2 = DeRefLink(node1->link[x]); // set HP
// Change the reference and at once increment the reference counter
// to the old node1 element
CompareAndSwapRef(&pNode->link[x],node1,node2);
ReleaseRef(node2); // clears HP
ReleaseRef(node1); // clears HP
goto retry; // a new reference also can be deleted, so we repeat
}
ReleaseRef(node1); // clears HP
}
}
Thanks to such change of accents of managing the lock-free container from the scheme core to the container element itself (it’s used well in virtual C++ functions) HRC scheme element itself becomes independent from a particularly implemented lock-free data structure. But you should note that CleanUpNode algorithm can break the data structure integrity for a short term as it changes references inside the element one by one, which can be unacceptable in some cases. We can use a program MultiCAS emulation for atomic application of all connections in the element for the lock-free containers which won’t accept such violation.
As well as for Hazard Pointers scheme, the number of retired elements is limited from the top. The algorithm of physical deletion is very similar to Scan algorithm of Hazard Pointers scheme (with some changes that are connected with reference counters management and CleanUpNode call). The main difference is the following: if it’s guaranteed in HP scheme (by choosing R > N = P * K) that Scan procedure will definitely delete something (there’s at least one retired element that is not guarded by the hazard pointer) Scan procedure call in HRC scheme can be a failure due to mutual elements references to each other (each reference is an increment of the counter). So if Scan fails we call CleanUpAll support procedure. It goes through all arrays of the retired pointers of all threads and calls CleanUpNode procedure for every for every remote element, thereby making the second Scan call successful. > Implementing HRC scheme in libcds > HRC scheme is implemented in libcds by analogy with the HP scheme. The main class is cds::gc::HRC. API of this class is absolutely analogous to cds::gc::HP API. > The main advantage of HRC scheme is possibility — embodying iterator concept – isn’t implemented in libcds. When working on the library I came to the conclusion that generally iterators are not applicable to lock-free containers. Iterators assume not only safe reference of the object iterator is pointing to, but also safe and round trip through the entire entire container. It’s impossible to provide the last condition (round trip) in lock-free containers in general case. There always will be a concurrent thread deleting the element our iterator is based on. As a result, it’s impossible to refer safely to the node fields, as the node is protected by the HP scheme and can’t be deleted physically. But you either can’t get the following element as the node can be removed from the lock-free container. > > Thus, HRC scheme is presented in libcds as a specific case of HP scheme implementation. By the example of it we can see that adding additional conditions (reference counter) makes HP scheme more complex. On test examples HRC container can be several times slower than HP container. You can also face the “buzz” which is common for full-fledged garbage collector. When it’s impossible to delete something during the Scan call(for example, due to circular references) we start CleanUpAll procedure running through all retired nodes. > HRC scheme is used in libcds as a variant of HP like schemes, which allows not to forget about generality during construction. Due to specific internal structure of HRC scheme generalization of HRC-based and HP-based containers is usually a very interesting task.
Pass the Buck
Working on the problem of memory reclamation in lock-free data structures Herlihy & al created Pass-the-Buck algorithm (PTB) [HLM02, HLM05], which is very similar to HP scheme of Michael M. But they essentially differ in implementation details.
As well as in HP scheme, The PTB scheme also requires declaring the pointer guarded (an analog of hazard pointer in HP scheme). PTB scheme is initially meant for indefinite in advance the number of guards (or hazard pointers). When there is enough retired data we call Liberate procedure, which is an analog of Scan in HP scheme. It returns the array of pointers which can be safely deleted. Unlike HP scheme, in which the array of retired pointers is private for the thread, the array of retired data is entire for all threads in PTB scheme. The structure of guard (hazard pointer) is interesting as it contains not only the guarded pointer but also the pointer to retired data, the so-called hand-off. If during deleting process Liberate procedure detects that some retired data are guarded, it places this retired record to the slot of hand-off guard. Hand-off data can de deleted during the next Liberate call if the guard they’re attached to has changed, meaning that it has a pointer to other guarded data.
In [HLM05] authors provide two algorithms for Liberate: wait-free and lock-free. Wait-free requires dwCAS (CAS over the double word), which makes the algorithm dependent on dwCAS support at the target platform. Lock-free algorithm is interesting by its ability to work only if the data change. If the data (guards and retired pointers) remain unchanged between the calls of lock-free Liberate version, circularity is possible (the algorithm won’t delete all possible retired data, so we’ll have to call it more and more times). The data remain unchanged in the end of the program when there’s a peeling being executed in the singleton destructor of PTB scheme, and also when we call Liberate.
Having bothered my head about circularity I decided to change Liberate algorithm of PTB scheme, making it by analogy with HP scheme. As a result, PTB implementation in libcds became more familiar to HP scheme variant with arbitrary number of hazard pointers and entire array of retired data. It hasn’t essentially affected the capability. The “clear” HP scheme is faster that PTB. But PTB can be preferable due to no restrictions to guards number.
Implementation in libcds In libcds library PTB scheme is presented by cds::gc::PTB class. Implementation details are located in cds::gc::ptb namespace. API of cds::gc::PTB is absolutely analogous to cds::gc:::HP, except for constructor arguments. The constructor accepts the following arguments:
PTB( size_t nLiberateThreshold = 1024, size_t nInitialThreadGuardCount = 8 );
- nLiberateThreshold — is threshold of Liberate call. As soon as the entire array of retired data reaches this size, we call Liberate
- nInitialThreadGuardCount — the initial number of guards when creating a thread (or rather when connecting the thread libcds internal infrastructure). In the next case of lacking guards the new ones are automatically created.
Summary
In this article I’ve reviewed algorithms of safe memory reclamation focusing on Hazard Pointer schemes. HP scheme and its variants represent quite a good way of providing safe memory control in the lock-free data structures. Everything mentioned above relates more to the area of creating lock-free data structures. If you’re just interested in libcds, it’s enough to initialize the chosen scheme and not to forget about attaching threads to it and replace scheme class as the first argument of GC container from libcds library. References guard, Scan() / Liberate() call, etc. – all of it is inside the container implementation. I’ve left one more algorithm overboard – RCU. It differs from HP-like schemes, but I’ll tell you about it in one of the following articles.
References
- [Fra03] Keir Fraser Practical Lock Freedom, 2004; technical report is based on a dissertation submitted September 2003 by K.Fraser for the degree of Doctor of Philosophy to the University of Cambridge, King’s College
- [GPST05] Anders Gidenstam, Marina Papatriantafilou, Hakan Sundell, Philippas Tsigas Practical and Efficient Lock-Free Garbage Collection Based on Reference Counting, Technical Report no. 2005-04 in Computer Science and Engineering at Chalmers University of Technology and Goteborg University, 2005
- [Har01] Timothy Harris A pragmatic implementation of Non-Blocking Linked List, 2001
- [HLM02] M. Herlihy, V. Luchangco, and M. Moir The repeat offender problem: A mechanism for supporting dynamic-sized lockfree data structures Technical Report TR-2002-112, Sun Microsystems
- Laboratories, 2002.
- [HLM05] M.Herlihy, V.Luchangco, P.Martin, and M.Moir Nonblocing Memory Management Support for Dynamic-Sized Data Structure, ACM Transactions on Computer Systems, Vol. 23, No. 2, May 2005, Pages 146–196.
- [Mic02] Maged Michael Safe Memory Reclamation for Dynamic Lock-Free Objects Using Atomic Reads and Writes, 2002
- [Mic03] Maged Michael Hazard Pointers: Safe Memory Reclamation for Lock-Free Objects, 2003
- [MS98] Maged Michael, Michael Scott Simple, Fast and Practical Non-Bloking and Blocking Concurrent Queue Algorithms, 1998
- [Tor08] Johan Torp The parallelism shift and C++’s memory model, chapter 13, 2008
Ropes — Fast Strings
Comments
Aleksey Kladov
Epoch based scheme is used in Crossbeam library for Rust: aturon.github.io/blog/2015/08/27/epoch/. Maybe the problem is solved there.